Ein Beitrag von
Sönke hat 100.000 Seemeilen Erfahrung im Kielwasser und von 2007 bis 2010 zusammen mit seiner Frau Judith die Welt umsegelt. Er veranstaltet diverse Seminare auf Bootsmessen (siehe unter Termine) und ist Autor der Bücher "Blauwassersegeln kompakt", "1200 Tage Samstag" und "Auszeit unter Segeln". Sönke ist zudem der Gründer von BLAUWASSER.DE und regelmäßig mit seiner Frau Judith und seinen Kindern auf der Gib'Sea 106 - HIPPOPOTAMUS - unterwegs.
Beim Navigieren gibt es eine interessante Komponente, die insbesondere auf langen Passagen – wie Ozeanüberquerungen – eine Rolle spielt: Der Kurs zwischen zwei Punkten kann auf zwei Wegen bestimmt werden. Entweder auf der Orthodrome oder auf der Loxodrome.
Das bedeutet Folgendes: Alle Seekarten haben gemein, dass unsere dreidimensionale Erdkugel auf einer zweidimensionalen Ebene abgebildet wird. Dabei kommt es in fast allen Fällen zu Abweichungen der Karte von der Realität. Am weitesten verbreitet ist die Seekarten-Projektion nach Mercator. Bei ihr haben auf der Karte alle Längengrade den gleichen Abstand zueinander, während die Abstände zwischen den Breitengraden zu den Polen hin zunehmen (weswegen Seemeilen am Kartenrand ja auch immer auf Höhe der Position abgesteckt werden sollten). Wird hier ein Kurs zwischen zwei Punkten abgesteckt und eine gerade Kurslinie gezogen, schneidet die Linie alle Längengrade im selben Winkel. Diese Variante der Routenermittlung folgt der Loxodrome. Auf der Karte ist das optisch die kürzeste Strecke — nämlich eine Gerade. Und genau das haben wir ja in der Schule gelernt: Die kürzeste Verbindung zwischen zwei Punkten ist eine Gerade. In der Geometrie stimmt das. Bei der Mercator-Projektion mit den zu den Polen hin immer weiter auseinander gezogenen Breitengraden stimmt das so nicht. In Wahrheit gibt es noch einen kürzeren Weg als die Loxodrome.

Papier-Seekarte mit Mercator-Projektion. Die Kurslinie schneidet alle Längengrade im selben Winkel.

Gleiche Seekarte, „unterschiedliche“ Meilen. Am oberen Rand misst die Seemeile 45 mm am unteren hingegen 36 mm.
Der tatsächlich kürzeste Weg zwischen zwei Punkten auf unserer Erdkugel, liegt auf dem größtmöglichen Kreis auf der Oberfläche – der Orthodrome. Ihr Durchmesser stimmt mit dem Erddurchmesser überein und ihr Mittelpunkt ist der Erdmittelpunkt. Sie teilt die Erde somit in zwei Hälften und hat vereinfacht gesagt immer eine Länge von 21.600 Seemeilen (360 Grad x 60 Bogenminuten bzw. 60 Seemeilen). Faktisch stimmt das nicht ganz, da unsere augenscheinlich runde Erde auch ein wenig unförmig ist. Das kann aber an dieser Stelle vernachlässigt werden.

Die kürzeste Verbindung zwischen zwei Punkten auf der Erde ist die Orthodrome.
Der bekannteste Großkreis auf der Erde ist der Äquator. Aber auch die Längengrade folgen allesamt einem Großkreis. Die Breitengrade hingegen sind – mit Ausnahme des Äquators – keine Großkreise, weil sie nicht durch den Mittelpunkt der Erde gehen und zu den Polen hin kleiner werden. Man nennt sie entsprechend auch Kleinkreise. So beispielsweise auch die Polarkreise auf 66,57 Grad Nord bzw. Süd. Sie sind nur etwa 8.600 Seemeilen lang.

Augenscheinlich ist die Erde nicht rund. Naja, halt nur augenscheinlich 😉
Wer Langeweile hat, kann das ganz praktisch mit einer kugelförmigen Frucht ausprobieren. Etwa einer Melone. Auf ihr werden zwei Punkte markiert. Dann wird sie so halbiert, dass zwei exakt gleich große Hälften entstehen und die beiden Punkte dabei auf der Schnittlinie liegen. In der Folge geht der Schnitt unweigerlich auch durch den Mittelpunkt der Melone. Übertragen auf unsere Erde bedeutet dies, dass wir an der Schnittlinie entlang segeln müssen, wenn wir den kürzesten Weg zwischen den beiden Punkten nutzen wollen.


Der kürzeste Weg zwischen Punkten liegt auf der Schnittlinie wenn die Kugel halbiert wird.
Im Umkehrschluss bedeutet dies: Sofern der Kurs nicht exakt dem Äquator folgt oder genau in Nord-Süd-Richtung bzw. Süd-Nord-Richtung verläuft, also einem Längengrad folgt, ergibt der kürzeste Weg zwischen zwei Punkten auf der Mercator-Karte immer eine Kurve (Orthodrome). Das hat zur Folge, dass während der Überfahrt nach und nach der Kurs zum Ziel geändert werden muss. Das klingt wie ein Umweg. Allerdings ist der augenscheinliche Umweg kürzer!

Routenberechnung im Vergleich. Rot: Loxodrome (länger), Blau: Orthodrome (kürzer).
Die beiden Begriffe Orthodrome und Loxodrome stammen übrigens aus dem Griechischen. Während „dromos“ für Lauf steht, bedeutet „orthos“ gerade und „loxos“ schief. Wir haben es also mit einem geraden und einem schiefen „Lauf“ zu tun. In der Blauwasserpraxis heißt die „gerade“ Orthodrome umgangssprachlich „Großkreis“ und auf Englisch entsprechend „Great Circle Line“. Das liegt nahe, da sie ja dem größtmöglichen Kreis auf der Erdoberfläche folgt. Die schiefe Loxodrome hingegen wird passend zur Mercator-Projektion „Kursgleiche“ oder auch „Kurve konstanten Kurses“ genannt, da sie wie beschrieben alle Längengrade im gleichen Winkel schneidet und somit immer der gleiche Kurs anliegt. Im Englischen heißt sie „Rhumbline“.
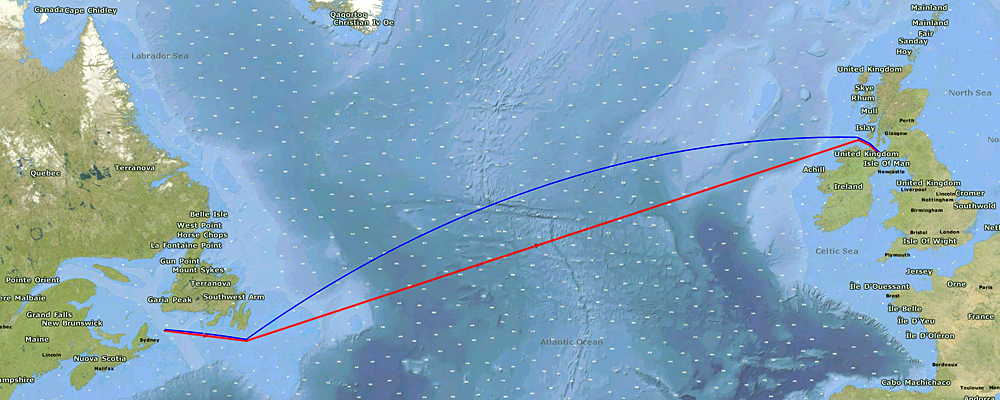
In Navigationsprogrammen wie MaxSea TimeZero kann man beide Routen im Vergleich betrachten.
Wer schon einmal mit dem Flugzeug eine Langstrecke geflogen ist und den Bordmonitor beobachtet hat, kennt das Phänomen übrigens. Beispielsweise fliegt ein Flugzeug von Hamburg nach New York meistens nicht den auf der Karte optisch direkten Weg (Kursgleiche), sondern einen Kreis, der zum Nordpol hin gewölbt ist, weil das der kürzeste Weg ist (Großkreis). Je dichter wir uns an den Polen befinden, desto stärker tritt der Effekt in Erscheinung. Umgangssprachlich wird daher für die Orthodrome auch gerne mal der Begriff „Luftlinie“ verwendet.


Flug-Route Hamburg – New York. Oben: Loxodrome, 4736 Sm, 257°. Unten: Orthodrome, 4683 Sm, 293°. Delta 51 Sm.
Doch was bedeutet das alles für die eigene Törnplanung? Ganz einfach: Auf einer Ozeanüberquerung in den hohen Breiten ist es sinnvoll, diese Gegebenheit zu berücksichtigen, da ein Kurs auf der Großkreisroute die Strecke durchaus signifikant verkürzen kann. Während der Unterschied auf einem Törn von Tasmanien zum Kap Hoorn rund 500 Seemeilen beträgt, sind es auf einem Törn von den Kanaren in die Karibik nur 25 Seemeilen.
Wer diesen Effekt nutzen möchte, wird mit einer einfachen Bleistiftlinie in der Papierseekarte an seine Grenzen stoßen. Etwa auf einem Übersegler zwischen den Kanaren und der Karibik. Wie soll man hier mit einfachen Bordmitteln wie Meilenzirkel und Kursdreieck den Großkreis bestimmen? Glücklicherweise gibt es im Zeitalter von Elektronik an Bord GPS, Plotter oder Navigationsprogramme mit elektronischen Seekarten. Sie nehmen dem Navigator diese Arbeit ab. Wichtig ist, dafür in den Einstellungen zu vermerken, nach welchem Verfahren der Kurs ermittelt werden soll. Dazu gibt es in der Regel eine Einstellung im Menü, bei der zwischen der Kurberechnung nach Loxodrome oder Orthodrome gewählt werden kann.

Bei vielen Navigationsprogrammen (hier MaxSea) kann in den Optionen die Berechnungsart gewählt werden.
Achtung! Ein auf der Papierseekarte augenscheinlich freier Weg, der auf dem üblichen Weg nach der Kursgleichen eingezeichnet wurde, kann bei einer Berechnung nach Großkreis einen deutlich nördlicher oder südlicher verlaufenden Bogen einschlagen und es können dann Hindernisse wie Atolle oder Inseln auf dem Weg liegen. Hier helfen elektronische Seekarten, um den Kurs zu überprüfen. Wurde er nach Großkreis berechnet, wird er in der Karte auch entsprechend dargestellt. Vor allem bei Vektorkarten, die kleine Hindernisse auf hohen Zoomstufen nicht anzeigen, ist es von elementarer Bedeutung den Track zu prüfen.
Eine Alternative sind theoretisch Karten mit gnomonischer Projektion. Auf ihnen sind die Längengrade gerade Linien, die zu einem Pol hin laufen. Die Breitengrade sind hingegen als Kurven dargestellt. Diese Karten sind sozusagen großkreistreu. Das bedeutet: Wer von A nach B navigieren möchte und eine solche Karte verwendet, kann die Großkreisroute durch Verbinden der Punkte A und B auf der Karte mit einer Geraden bestimmen. In der Praxis haben wir allerdings noch kein Schiff getroffen, das solche Karten an Bord hatte. Das lag vielleicht aber auch daran, dass wir auf Langfahrt noch nicht so oft in den ganz hohen Breiten unterwegs waren.

Karten mit gnomonischer Projektion sind großkreistreu. Quelle der Karte: Wikipedia.
Mit anderen Worten: Wer einen Törn in hohen Breiten über lange Distanzen von Ost nach West oder umgekehrt plant, sollte einen Kurs auf der Großkreisroute in Erwägung ziehen, da der beschriebene Effekt dann am stärksten auftritt und eine Törnplanung auf der Großkreisroute signifikant kürzer sein kann. Allerdings ist das nur dann sinnvoll, wenn es die Seemannschaft auch erlaubt. Es nützt ja nichts, einen Eisberg zu rammen, nur weil der kürzeste Weg zwischen Tasmanien und Kap Hoorn durch die Antarktis führt.

Die kürzeste Route zwischen Tasmanien und Kap Hoorn führt bis auf 70 Grad Süd.
Selbstverständlich müssen wir Blauwassersegler nicht alles mitmachen, was die Technik uns bietet. Gerade auf der beliebten Barfußroute, die ohnehin schon – im weitesten Sinne – dem Großkreis Äquator folgt, ist der Effekt nicht sehr groß und meistens kommt es auf ein paar Seemeilen mehr oder weniger während einer Atlantiküberquerung nicht an. Regattasegler hingegen werden vermutlich immer dem Großkreis folgen. Egal, ob es dabei um die Welt oder auf dem heimischen Baggersee bis zur nächsten Boje geht 😉
Weiterführende Beratung (WERBUNG)
Eine ausführliche, weiterführende Beratung zum Thema “Navigation” kannst du bei einem der folgenden Anbieter bekommen:
























