Ein Beitrag von
Mathias hat seine berufliche Tätigkeit als Senior Fellow für Chip-Sicherheit vorübergehend reduziert und segelt seit dem Sommer 2019 mit seiner Frau Birte auf dem Trimaran SAN, einer NEEL 51, um die Welt.
Einleitung
Über das richtige und sichere Ankern ist schon viel geschrieben worden. Etwa im Segler Lexikon von Joachim Schult. Da finde ich unter dem Eintrag „Kettenkurve” eine kurze Beschreibung, die mit der Empfehlung endet, die vierfache Wassertiefe als Kettenlänge beim Ankern sei optimal. Bobby Schenk wiederum empfiehlt in seinem Buch „Ankern“ im Allgemeinen die fünffache Wassertiefe und nur bei großen Wassertiefen von 20 und mehr Metern die dreifache Wassertiefe als Kettenlänge.
Einen anderen Ansatz verfolgen Sönke und Judith Roever in ihrem Buch „Blauwassersegeln Kompakt“ beziehungsweise in diesem Beitrag über das Ankern: Ihrer Empfehlung nach ergibt sich die Kettenlänge aus der Wassertiefe, zu der dann eine Konstante hinzuaddiert wird. Die Konstante liegt zwischen 25 und 35 Metern. Bei viel Wind entsprechend mehr.

Dies sind alles sehr wertvolle Beiträge, aber als technisch versierte Person hat es mich immer verwundert, dass es meist nur solche doch recht vagen Aussagen zur benötigten Kettenlänge gibt, und diese überwiegend die Windstärke und das Gewicht der Kette vollkommen ignorieren.
Bei meiner Recherche zu diesem Beitrag habe ich angenommen, dass es doch zumindest bei der Britischen Admiralität genauere Vorschriften geben muss, wie lang eine Ankerkette zu sein hat. Wenn die Seefahrernation keine Vorgaben hat – wer dann?
Einer der wenigen öffentlich verfügbaren, technischen Beiträge stammt von Peter Smith, aber dort werden im Wesentlichen nur numerische Ergebnisse zu Computer-Simulationen gezeigt, und es ist nicht einfach, diese auf das eigene Schiff zu übertragen. Dies möchte ich in diesem kleinen Beitrag ändern.

Um es gleich klarzustellen: Ich mache hier keinerlei Aussagen zur Haltekraft von Ankern — dazu gibt es einschlägige Praxistests —, es geht nur um die „wirklich” minimal benötigte Kettenlänge zum Ankern, wenn der Anker als haltend angenommen wird und die Kette (immer noch) waagerecht am Anker ansetzen soll, um dessen Haltekraft nicht zu schmälern. Diese minimal benötigte Kettenlänge wird von der Wassertiefe, aber auch von der Windstärke abhängen. Den Einfluss von Wellengang werde ich in diesem Beitrag zunächst vernachlässigen. Er kann später pauschal durch einen Sicherheitsaufschlag bei der Windstärke berücksichtigt werden.
Das Ergebnis ist überraschend einfach:

L ist die benötigte Kettenlänge, Y die Ankertiefe, und a ein Parameter, der vom Schiff und der Windstärke abhängt, aber nur einmal tabelliert werden muss.
Als Spezialfall dieser allgemeinen Kettenkurve findet sich auch die obige Regel „X Meter Kette pro Meter Wassertiefe” wieder. Sie beschreibt letztendlich nur den Extremfall einer vollkommen gestrafften Kette bei Sturm, wenn die Kette nicht mehr waagerecht am Anker angreift, sondern mit der Steigung 1 : X.
Die Roever’sche Faustformel findet man als Näherung für große Ankertiefen und moderaten Wind wieder, wobei der genaue Wert der Konstanten sowohl von der Größe des Schiffes als auch von der Windstärke abhängt.

Abbildung 1 zeigt: Die minimal benötigte Ankerkettenlänge L bei maximaler Haltekraft des Ankers in Wassertiefe Y ergibt sich, wenn die Kette schon nicht mehr am Meeresboden aufliegt, aber am Anker noch immer genau waagerecht angreift. FW ist die am Schiff angreifende Windkraft und FK das Gewicht der Kette im Wasser. Der Punkt (x1,y1) ist gedacht zur Diskussion eines Ankers, an dem die Kette nicht mehr waagerecht angreift, sondern mit einer Steigung b. In diesem zweiten Fall ist die Ankertiefe nur noch y2.
Etwas Mathematik zur Bestimmung der Ankerkettenlänge
Die Fragestellung, wie eine Kette unter dem Einfluss der Schwerkraft durchhängt, ist schon seit vielen Jahrhunderten erforscht und gelöst. Schon Christiaan Huygens und Johann Bernoulli haben sich hiermit 1690/91 beschäftigt. Siehe Wikipedia
Es ist ein Problem der Variationsrechnung in der Mathematik und eine gern gestellte Übungsaufgabe in der Theoretischen Mechanik im Physikstudium, welches wir hier aber nicht lösen wollen. Es stellt sich heraus, dass eine Kette, ein Tau oder ähnliches unter dem Einfluss der Schwerkraft immer die gleiche prinzipielle Form annimmt,

Die Parameter a, x0 und y0 sind noch zu bestimmen, und der Ausdruck cosh() beschreibt die sogenannte cosinus hyperbolicus Funktion, welche für (x – x0)2 << 5a2 in erster Näherung eine Parabel ist (Das Zeichen << bedeutet „sehr viel kleiner als”).
Es ist leicht einzusehen, dass eine idealisierte Ankerkette auch immer diese Form annehmen muss. Eine solche Ankerkette besitzt in erster Näherung eine konstante Masse m pro laufendem Meter, auf welche die Schwerkraft wirkt, und sie muss — bei Vernachlässigung des Wellengangs — die am Schiff angreifende horizontale Windkraft von ihrem einen Ende in den Anker am anderen Ende der Kette umleiten. Dabei kann die Kette an jedem Punkt immer nur Kräfte entlang ihrer dortigen Richtung aufnehmen und weitergeben, es können also insbesondere keine seitlichen Scherkräfte aufgenommen werden, und aus genau dieser Eigenschaft heraus ergibt sich ihre charakteristische Form.

Im Folgenden möchte ich die minimal benötigte Kettenlänge L bestimmen als Funktion der Wassertiefe Y am Ort des Ankers, des Gewichts FK der Kette und der Windkraft FW, die auf das Schiff einwirkt — und zudem unter der vereinfachenden Annahme, dass es keinerlei Wellengang gibt.
Die Haltekraft des Ankers soll noch nicht beeinträchtigt sein, also muss die Kette gerade so lang sein, dass sie eben nicht mehr auf dem Meeresboden herumliegt, aber immer noch waagerecht am Anker angreift. In diesem Fall sitzt der Anker im Minimum der cosh() Funktion, also bei x0, wo die Steigung dieser Funktion verschwindet, und wir können ohne Einschränkung der Allgemeinheit x0 = 0 setzen, wie in Abbildung 1 veranschaulicht.
Hervorzuheben ist, dass in diesem Fall die Kette immer noch exakt waagerecht am Anker angreift und somit der Anker maximal halten kann. In diesem kleinen Detail liegt Bobby Schenk falsch, wenn er in seinem ansonsten sehr schönen Buch zum Ankern auf Seite 16 unten behauptet, dass eine Kette unendlich lang sein müsste, um waagerecht am Anker angreifen zu können. Dem ist einfach nicht so. Aber sie müsste schon sehr lang werden, wenn es so richtig bläst …
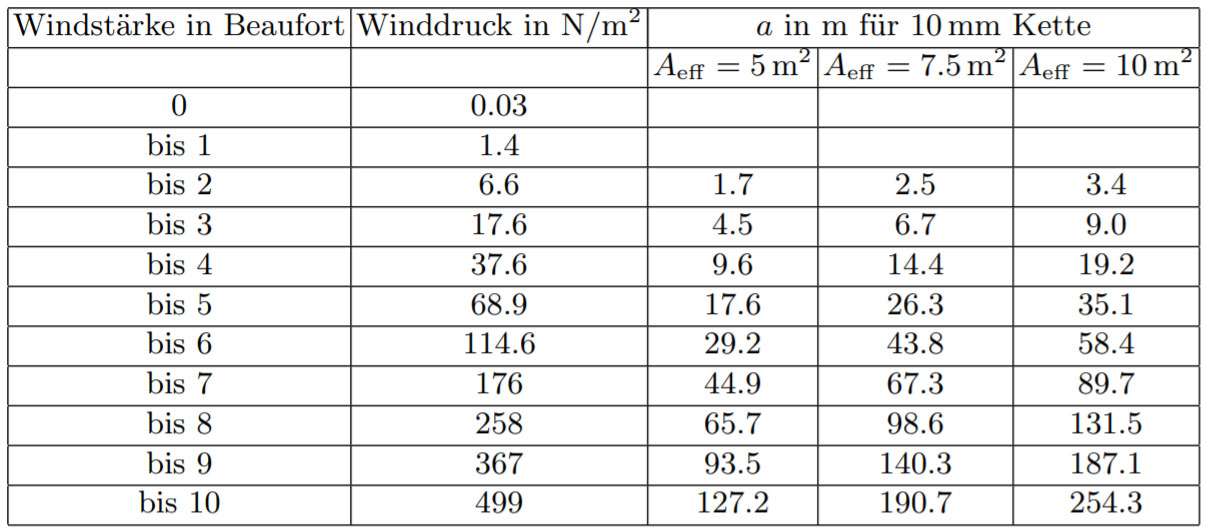
Tabelle 1 zeigt Winddrücke auf eine Fläche mit cp = 1 bei 20 Grad Celsius auf Meereshöhe. Im Vorgriff auf die Gleichungen 7 und 8 ist auch noch der Parameter a für eine 10 mm Stahlkette und Aeff = 5 m2, Aeff = 7,5 m2 sowie Aeff = 10 m2 aufgeführt. Andere Werte des Parameters a erhält man durch lineare Interpolation von Aeff.
Wie bestimmen wir nun die Parameter a und y0? Am einfachsten legen wir das Koordinatensystem so, dass am Anker x = 0 und y = 0 ist (siehe Abbildung 1), womit sich wegen cosh(0) = 1

ergibt. Mit Großbuchstaben X und Y bezeichnen wir nun den Punkt, an dem die Ankerkette die Wasseroberfläche durchbricht. Damit ist X etwas kleiner als der vom Schiff benötigte Schwoikreisradius. Die Kettenlänge bis zu diesem Punkt (X,Y) errechnet sich als
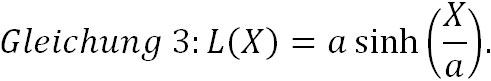
Durch geschicktes Quadrieren beider Gleichungen und Umstellen erhält man unter Zuhilfenahme von cosh2(z) − sinh2(z) = 1 für beliebiges z,

Dies ist das zentrale Ergebnis dieses Beitrages. Für a² << (Y + a)², also sehr große Wassertiefen oder sehr geringe Windkräfte, gilt damit in erster Näherung wie erwartet L ≈ Y + a. Die Kette hängt also fast senkrecht nach unten. Dies hat im Grunde genommen Ähnlichkeit mit der Roever’schen Faustformel auf S. 112 ihres Buches „Blauwassersegeln kompakt“, L = Y + 5 m + 20…30 m, wenn wir a ≈ 25…35 m ansetzen.
Da, wie im Folgenden ersichtlich werden wird, der Parameter a jedoch von der Größe des Schiffes und von der Windstärke abhängt, muss man diese Roever’sche Formel immer auf das eigene Schiff und die jeweilige Situation anpassen — und sie ist nur eine Näherung.
Im umgekehrten Grenzfall für 2a >> Y, also bei Sturm und/oder sehr geringer Ankertiefe, erhalten wir in erster Näherung

In diesem Fall nimmt die benötigte Kettenlänge also nur mit der Wurzel der Wassertiefe zu. Auch hier ist es also besser, bei geringer Wassertiefe zu ankern, aber der Effekt ist relativ schwach: Wenn die Ankertiefe auf ein Viertel abnimmt, verringert sich die benötigte Kettenlänge nur auf die Hälfte. In keinem Szenario nimmt die Kettenlänge jedoch mit der dreifachen Wassertiefe zu. L = 3Y gilt nur für einen einzigen Punkt auf der Kettenkurve, Y = a/4. Im allgemeinen Fall erhält man nach Lösen der quadratischen Gleichung 4 wieder eine nicht-lineare Abhängigkeit zwischen Kettenlänge und Ankertiefe,

Mit dieser Formel kann ich also bei gegebener maximaler Kettenlänge und gegebenem Parameter a die maximal mögliche Ankertiefe errechnen, bei der die Kette immer noch waagerecht am Anker angreift.
Wie bestimmen wir nun den verbleibenden Parameter a? Zunächst ist die Ableitung der Kettenkurve aus Gleichung 2 bei Punkt (X,Y) wegen fehlender Scherkraft gegeben durch ein Kräfteparallelogramm, genauer gesagt dem Verhältnis von Kettengewicht zu Windkraft,

wobei FK = −Lmg das Gesamtgewicht der Kette vom Anker bis zum Punkt (X,Y) ist, mg das Gewicht der Kette pro laufendem Meter im Wasser, also um den Auftrieb im Wasser reduziert, FW die angreifende Windkraft, und wie üblich g = 9,81m/s2, die Gravitationsfeldstärke auf der Erdoberfläche.
Aus den beiden Gleichungen 3 und 6 ergibt sich durch Einsetzen und Eliminieren von L der verbleibende Parameter a zu

also dem Verhältnis von Windkraft zu spezifischem Gewicht der Kette pro laufendem Meter im Wasser. Damit haben wir alle Kettenparameter vollständig bestimmt. Die einzige Unbekannte ist nun die am Schiff angreifende Windkraft FW. Laut Wikipedia können wir dafür

setzen, wobei A die Angriffsfläche ist, die das Schiff dem Wind bietet, cp der Druckbeiwert ist, der die Windschnittigkeit des Schiffes beschreibt, und pstau der Staudruck des Windes auf eine senkrechte Fläche ist.
Letztendlich interessiert uns jedoch nur das Produkt Aeff = cpA, welches wir als eine effektive Windangriffsfläche des Schiffes interpretieren können, die wir entweder schätzen müssen, oder auch experimentell bestimmen können — siehe weiter unten.

Der Staudruck hängt klarerweise von der Stärke des Windes ab. Auf Wikipedia gibt es Angaben bezogen auf die Beaufort Skala (in Tabelle 1 wiedergegeben), wobei hier immer der Staudruck am oberen Ende des jeweiligen Beaufort-Bereiches angegeben ist.
Die Kettenkurve ist damit nur vom Parameter a = (Aeff pstau)/(mg) abhängig, also dem Verhältnis von der am Schiff angreifenden Windkraft zu dem Kettengewicht pro laufendem Meter im Wasser.
Beispiele für die „richtige“ Länge der Ankerkette
Im Folgenden habe ich die benötigte minimale Kettenlänge L für einige gebräuchliche Kettenstärken, verschiedene effektive Windangriffsflächen Aeff und Windstärken von 3 bis 10 Bft mit Hilfe der Gleichungen 4 und 7 geplottet. Wie vorher angemerkt, ist dies immer die Länge L(Y) bis zu dem Punkt (X,Y) in Abbildung 1, an dem die Ankerkette die Wasseroberfläche durchbricht, und es sind demzufolge in Abhängigkeit vom Freibord des Schiffes und des Winkels, mit dem die Kette aus dem Wasser kommt, noch einige Meter Kette hinzuzuaddieren, um die benötigte Gesamtkettenlänge zu erhalten. Oder man rechnet die Wassertiefe Y einfach von der Höhe des Bugs aus — der kleine Fehler, dass die Kette auf dem Stück bis zur Wasseroberfläche schwerer ist als im Wasser, fällt nicht ins Gewicht.
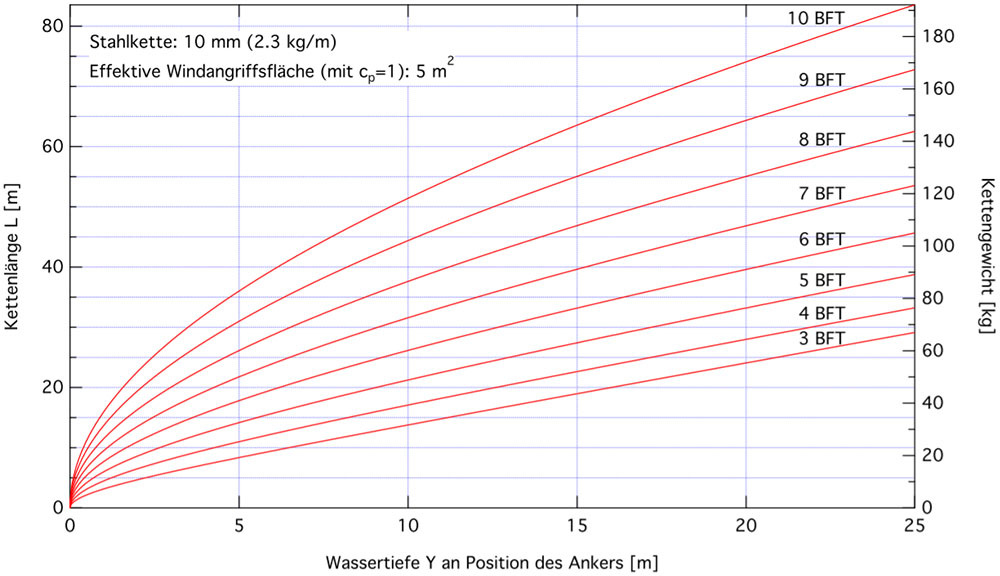
Abbildung 2 zeigt die minimal benötigte Kettenlänge L in Abhängigkeit von der Ankertiefe Y und verschiedenen Windstärken für eine Kette der Stärke 10 mm mit Aeff = 5 m2. Gewicht im Wasser: m = 2 kg/m.
Abbildung 2 gilt für ein kleineres Schiff mit einer effektiven Windangriffsfläche von nur Aeff = 5 m2 und einer für ein so kleines Schiff etwas überdimensionierten 10 mm Eisenkette, welche an Land ein Gewicht von 2.3kg/m für den laufenden Meter hat.
Wenn ich also beispielsweise auf einer Wassertiefe von 15 Metern ankern möchte, bei sieben Bft Wind, dann benötige ich mindestens 40 Meter Kette bis zur Wasseroberfläche, also etwas weniger als das Dreifache der Wassertiefe. Bei 9Bft Wind sind es schon 55 Meter Kette und damit deutlich mehr als das Dreifache der Wassertiefe. Die Regel „Drei Meter Kette pro Meter Wassertiefe” ist also nicht differenziert genug und berücksichtigt nicht den Einfluss des Windes.

Abbildung 3 zeigt die minimal benötigte Kettenlänge L in Abhängigkeit von der Ankertiefe Y und verschiedenen Windstärken für eine Kette der Stärke 10 mm mit Aeff = 7,5 m2. Gewicht im Wasser: m = 2 kg/m.
Natürlich ist es ratsam, als Windstärke nicht die mittlere Windstärke zu verwenden, sondern die Stärke der größten zu erwartenden Böen. Und wenn es stärkeren Wellengang gibt, sollte man noch eine oder zwei Windstärken oben drauflegen, da in den obigen Rechnungen die Kraft des Wellengangs nicht mit berücksichtigt worden ist.

Abbildung 4 zeigt die minimal benötigte Kettenlänge L in Abhängigkeit von der Ankertiefe Y und verschiedenen Windstärken für eine Kette der Stärke 10 mm mit Aeff = 10 m2. Gewicht im Wasser: m = 2 kg/m.
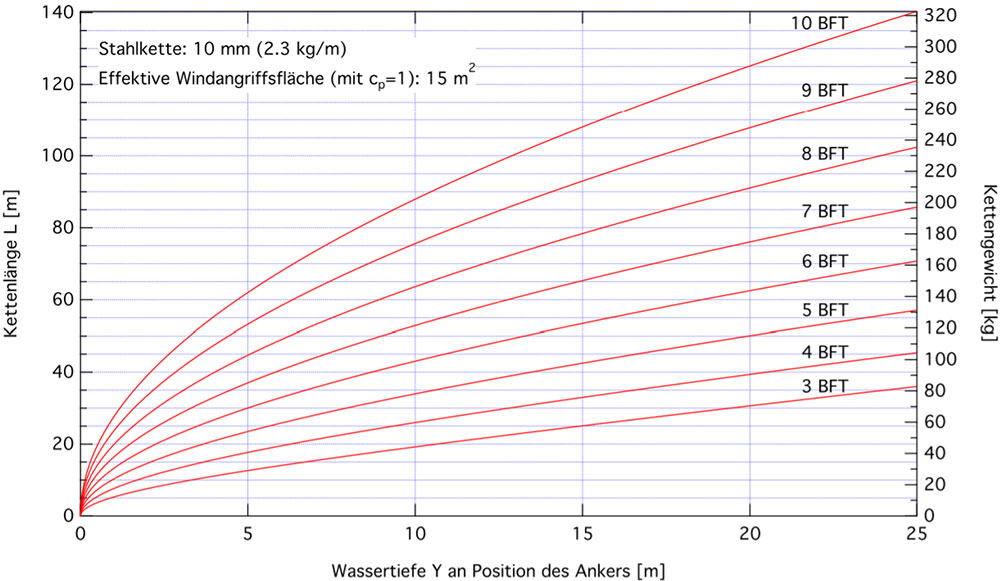
Abbildung 5 zeigt die minimal benötigte Kettenlänge L in Abhängigkeit von der Ankertiefe Y und verschiedenen Windstärken für eine Kette der Stärke 10 mm mit Aeff = 15 m2. Gewicht im Wasser: m = 2 kg/m.

Abbildung 6 zeigt die minimal benötigte Kettenlänge L in Abhängigkeit von der Ankertiefe Y und verschiedenen Windstärken für eine Kette der Stärke 10 mm mit Aeff = 20 m2. Gewicht im Wasser: m = 2 kg/m.
Des Weiteren sieht man in diesen Abbildungen auch sehr schön, dass für sehr kleine Wassertiefen die Kettenlänge mit der Wurzel der Ankertiefe steigt, während bei großen Wassertiefen die Kurve sich asymptotisch einer geraden Linie mit einem konstanten Offset annähert — der Roever’schen Faustformel.
In den Abbildungen 2 bis 6 habe ich entsprechende Kurven für verschiedene effektive Windangriffsflächen Aeff bis zu 20 m2 geplottet, allesamt für eine 10 mm starke Eisenkette. Auf der linken Skala ist immer die Kettenlänge angegeben und auf der rechten Skala das dazu entsprechende Gewicht dieser Kette.

Logischerweise benötigen größere Schiffe bei gleicher Kettenstärke längere Ketten, um auf der gleichen Ankertiefe ankern zu können. So muss man bei einem Schiff mit Aeff = 20 m2, was vielleicht einem ausgewachsenen Katamaran entspricht, bei 15 Meter Ankertiefe und 7 Bft Wind schon 75 Meter Kette stecken, also fast doppelt so viel Kette wie bei dem kleinen Schiff aus Abbildung 2 mit nur Aeff = 5 m2. Bei 20 Metern Ankertiefe sind es gut 87 Meter Kette.
Die Regel „Auf der Blauwasserroute braucht man mindestens 70 Meter Kette” ist also mit etwas Vorsicht zu genießen. Es hängt schlichtweg von der Größe des Schiffes ab — und von der verwendeten Kettenstärke. Je größer das Schiff und je leichter die Kette, desto länger muss die Kette sein.
In den Abbildungen 7 bis 10 habe ich dazu einige Ergebnisse geplottet für 8 und 13 mm Eisenketten. Bei ansonsten gleichen Bedingungen reduziert sich die minimale Kettenlänge L etwas, wenn man eine dickere und damit schwerere Kette wählt und umgekehrt.
Dies sollte jedoch nicht zu dem Trugschluss verleiten, besonders dicke Eisenketten zu verwenden, um so Kettenlänge und damit vermeintlich Kettengewicht zu sparen, weil dieser Effekt zu schwach ist, eine dickere Kette zu kompensieren. Dies kann auch an den jeweils rechten Skalen der Abbildungen gut erkannt werden. Es ist also besser, eine möglichst hochwertige Kette mit hoher Bruchlast zu verwenden, die dann entsprechend dünner sein kann. Das spart trotz längerer Kette am Gesamtgewicht.

Einziger Haken: Damit wird der Schwoikreisradius X damit dann auch größer, was bei einigen Ankerplätzen zu Problemen führen kann. Bei gleicher Ankertiefe und gleicher Kettenstärke benötigt ein großes Schiff einen größeren Schwoikreisradius als ein kleines Schiff, einfach weil es mehr Kette braucht. Dies ist bei der Einschätzung von Nachbarn am Ankerplatz und dem eigenen Abstand zu denselbigen mit zu berücksichtigen.

Abbildung 7 zeigt die minimal benötigte Kettenlänge L in Abhängigkeit von der Ankertiefe Y und verschiedenen Windstärken für eine Kette der Stärke 8 mm mit Aeff = 5 m2. Gewicht im Wasser: m = 1,22 kg/m.

Abbildung 8 zeigt die minimal benötigte Kettenlänge L in Abhängigkeit von der Ankertiefe Y und verschiedenen Windstärken für eine Kette der Stärke 8 mm mit Aeff = 7,5 m2. Gewicht im Wasser: m = 1,22 kg/m.

Abbildung 9 zeigt die minimal benötigte Kettenlänge L in Abhängigkeit von der Ankertiefe Y und verschiedenen Windstärken für eine Kette der Stärke 13 mm mit Aeff = 15 m2. Gewicht im Wasser: m = 3,4 kg/m.

Abbildung 10 zeigt die minimal benötigte Kettenlänge L in Abhängigkeit von der Ankertiefe Y und verschiedenen Windstärken für eine Kette der Stärke 13 mm mit Aeff = 20 m2. Gewicht im Wasser: m = 3,4 kg/m.
Abschließend — und mehr zur Abschreckung — seien auch noch einmal die entsprechenden Kurven einer Bleiankerleine gezeigt. Dies sind normale Trossen, in die etwas Blei eingearbeitet ist, entweder entlang der ganzen Trosse oder nur für die ersten paar Meter. Wir nehmen der Einfachheit halber an, das Blei ist entlang der ganzen Länge eingearbeitet.

Abbildung 11 zeigt die benötigte Bleiankerleinenlänge L in Abhängigkeit von der Ankertiefe Y und verschiedenen Windstärken für eine 12 mm (Durchmesser) starke Bleiankerleine von LIROS mit Aeff = 3 m2 . Gewicht im Wasser: m = 65 g/m
In Abbildung 11 wird ersichtlich, dass schon ein sehr kleines Schiff mit Aeff = 3 m2, ausgerüstet mit einer Standard-Bleiankerleine von 12 mm Querschnitt und 40 Meter Länge, wie sie beispielsweise von LIROS angeboten wird, nur auf sehr geringen Wassertiefen ankern sollte. Ich hatte lange einen Dragonfly 28 Sport und der ist mit einer solchen Ankerleine ausgestattet. Folglich habe ich immer versucht, mit so viel Ankerleine wie möglich auf nicht viel mehr als zwei Metern Wassertiefe und gutem Sandgrund zu ankern — Kielschwert eingezogen. Wahrscheinlich war hierbei ein nicht unbedeutender Sicherheitsfaktor, dass unser Delta-Anker mit 10 kg überdimensioniert ist, und er damit auch noch stark genug hält, wenn die Bleiankerleine schon nicht mehr exakt waagerecht an ihm zieht.
Die praktische Bestimmung des Parameters a
Der eine oder andere von euch wird sich nun sicherlich gefragt haben, wie denn die effektive Windangriffsfläche Aeff des eigenen Schiffes bestimmt werden kann.
Zum einen kann man diese sicherlich grob abschätzen über die Projektionsfläche des Schiffes von vorne und einem angenommen Windschnittigkeitsfaktor cp, aber es gibt auch eine genauere Methode: Hierbei ankert man bei verschiedenen Windstärken und verschiedenen Wassertiefen und misst nach (Tauchen!), wieviel Kette gesteckt werden muss, damit die Kette gerade eben nicht mehr auf dem Meeresboden aufliegt, sondern gleich am Anker anfängt, in Richtung Wasseroberfläche aufzusteigen. Der Einfachheit halber kann man natürlich auch einfach den Punkt nehmen, von dem die Kette sich vom Meeresboden abhebt: Wie tief ist das Wasser an dieser Stelle und wieviel Kette wird von hier bis zur Wasseroberfläche gebraucht?

Wer dies für verschiedene Windstärken und Wassertiefen — und möglichst wenig Wellengang — gemessen hat, kann damit den windabhängigen Parameter a und letztlich auch Aeff für sein Schiff bestimmen. Dann kann man sich die eigene Ankerkettenkurve ausdrucken und im Schiff geeignet aufbewahren.
Was passiert, wenn die Kette nicht mehr waagerecht am Anker angreift?
Ich gehe noch einen Schritt weiter und betrachte auch den Fall, dass die Kette nicht mehr waagerecht am Anker angreift, sondern mit einer gewissen Steigung b : 1. Wieviel Kette ist dann noch nötig?

Es gilt nach wie vor die gleiche Kettenkurve, nur dass nun der Anker „etwas weiter oben” an der Kettenkurve in Abbildung 1 angreift, sagen wir an einem Punkt (x1,y1), an dem die Steigung der Kettenkurve genau b beträgt. Wir müssen also nur die Länge L1 = L(x1) der Kette von (0,0) bis zum Punkt (x1,y1) ausrechnen und von der Gesamtlänge L der (nun zwischen (0,0) und (x1,y1) fiktiven) Kette abziehen. Gleiches gilt für die Tiefe y1.
Aus Gleichung 6 geht hervor, dass für die lokale Ableitung/Steigung

gilt und entsprechend daraus folgend

Mit Gleichung 2 erhalten wir unter Zuhilfenahme von cosh2(z) − sinh2(z) = 1

wobei die Näherung (ausgedrückt durch das Symbol ≈) für b << 1 gilt. Damit ergibt sich für einen Anker in Wassertiefe y2 = Y − y1, an dem die Kette mit Steigung b:1 angreift, die minimale Kettenlänge als

Man kann Y als die fiktive Ankertiefe interpretieren, die sich ergeben würde, wenn man die Kette auf die fiktive Länge L verlängert, um wieder einen Punkt zu finden, wo diese fiktive Kette waagerecht an einen Anker ansetzen würde.
In der Regel wird man hiermit vielleicht nicht sonderlich viel anfangen können, da nicht klar ist, wie stark die Haltekraft des Ankers beeinträchtigt wird, wenn die Kette nicht mehr waagerecht angreift. Aber beispielsweise im Falle der Bleiankerleine, oder aber auch generell in einem starken Sturm, wird es sich häufiger nicht vermeiden lassen, dass die Ankerleine nicht waagerecht angreift, und dann kann es nützlich sein zu wissen, wieviel Ankertiefe man auf diesem Wege „gewinnen” kann — zumal wenn der Anker überdimensioniert ist.
Beispiel Bleiankerleine
Dazu ein Beispiel mit der Bleiankerleine: Für die 12 mm-Bleiankerleine habe ich im Wasser ein Nettogewicht von 65 g pro laufendem Meter gewogen. Bei 6 Bft ergibt sich damit für Aeff = 3 m2 ein Wert von a = 539m. Nehmen wir nun beispielsweise eine Steigung von b = 0,1 an, also 10 Zentimeter pro Meter, dann ergibt sich mit den Gleichungen 10 und 11, dass L1 = 53,9 Meter und y1 = 2,7 Meter ist.
Wenn wir eine reale Ankerleine von L2 = 40 m zur Verfügung haben, dann ist die fiktive Kettenlänge L = L1 + L2 = 93,9 Meter. Für diesen Wert ergibt sich nach Gleichung 5 ein Wert von Y = 8,1 Meter. Hiermit berechnet sich die maximale Ankertiefe zu immerhin y2 = Y − y1 = 5,4 Meter.
Bei einer waagerecht angreifenden Ankerleine wäre die Ankertiefe für eine 40 Meter lange Ankerleine bei 6 Bft jedoch nur 1,5 m gewesen — zu flach, selbst für den Dragonfly 28, um ruhig schlafen zu können!

Nicht zu vergessen ist in beiden Fällen, dass die hier berechnete Länge der Bleiankerleine nur bis zu dem Punkt reicht, an dem sie die Wasseroberfläche durchbricht. Im vorliegenden Fall ist der Winkel der Leine aber sehr flach, und deshalb sind noch recht viele Meter Leine bis zur Klampe am Bug oder zum Hahnepot hinzuzurechnen. Alternativ kann auch die Freibordhöhe am Bug/Hahnepot von der maximalen Ankertiefe y2 abgezogen werden, auch wenn dies etwas zu konservativ ist, da die Bleiankerleine außerhalb des Wassers fast dreimal schwerer ist als im Wasser und sich somit außerhalb des Wassers deutlich stärker krümmt.
Jedenfalls bleibt von den obigen 1,5 Metern Wassertiefe bei dem Dragonfly 28 mit Hahnepot dann noch etwa 1 Meter Tiefe zum Ankern übrig. Mit b = 0,1 wären es immerhin 4,9 Meter.
Beispiel 10 mm Eisenkette
Annahme: Bei einer 10 mm starken Eisenkette und einer Aeff von 15 m2 stehen wieder L2 = 40 Meter Kette zur Verfügung. Mit dem gleichen Wert von b und ebenfalls 6 Bft Wind ergibt sich zunächst a = 87,6 Meter und damit L1 = 8,8 Meter sowie y1 = 0,44 Meter. Hieraus folgt eine fiktive Ankerkettenlänge von L = L1 + L2 = 48,8 Meter und somit nach den Gleichungen 4 und 5 eine maximale Ankertiefe von y2 = Y − y1 = 12,3 Meter.
Eine waagerecht am Anker angreifende Kette von 40 Metern Länge hingegen hätte nur eine maximale Ankertiefe von 8,7 Metern erlaubt. Der Effekt ist also relativ betrachtet kleiner als bei der Bleiankerleine, aber immer noch relevant.
Im Extremfall eines sehr starken Sturms wird die Kette vollkommen straff gespannt sein, wodurch sich die Steigung b am Anker bis zum Bug des Schiffes fortsetzt. Dies ist das einzige Szenario, in dem es Sinn macht, von einem festen Verhältnis zwischen Ankertiefe und Kettenlänge zu reden — es ist einfach vorgegeben durch die Steigung b.
Ob dieses Verhältnis nun 1:3 oder 1:8 ist, hängt schlicht davon ab, wieviel Haltekraft dem Anker unter den gegebenen Verhältnissen zugetraut wird, aber das soll nicht Gegenstand dieses Beitrags sein. J
Diese ganzen Überlegungen kann man natürlich nun auch umdrehen und sich fragen: Bei gegebener Kettenlänge L2 und Ankertiefe y2, sowie bei gegebener Windkraft, also a, wie groß ist dann die Steigung b der am Anker angreifenden Kette?
Welchen Einfluss hat ein Reitgewicht?
Gelegentlich wird empfohlen, ein Reitgewicht an der Kette zu befestigen, um so die effektive Kettenlänge zu erhöhen (siehe Abbildung 12). Der Effekt dieser Maßnahme ist im Rahmen des obigen Modells sehr einfach zu beschreiben: Es wird an die Kette eine Punktlast angehängt, die einen Knick in der Kettenlinie bewirkt.

Wenn ein Reitgewicht FR am Punkt (xR, yR) befestigt wird, dann ergibt dies den angesprochenen Knick in der Kettenlinie. Genauer betrachtet zeigt sich, dass man den weiteren Kettenverlauf zur Wasseroberfläche einfach dadurch erhält, dass man eine Kopie (gelb in Abbildung 12) der ursprünglichen Kettenlinie um den Vektor DR so verschiebt, bis das Gewicht einer Kette der Länge LR − L1 dem Gewicht des Reitgewichts (im Wasser) entspricht: FR = m(LR − L1). Klarerweise ist L2 < L‘2, und dies ist einer der positiven Effekte eines Reitgewichts.
Um die Größe dieses Knicks zu berechnen, muss man nur verstehen, dass an jedem Punkt entlang der Kette die nach unten wirkende Gewichtskraft dem Gewicht der Kette zwischen diesem Punkt und dem Anker entspricht (genauer dem Punkt, wo die Kette auf dem Untergrund aufkommt).
Ein Reitgewicht FR bewirkt also, dass dieser Kettenabschnitt virtuell um FR/m Meter verlängert wird, wobei m das spezifische Gewicht der Kette pro laufendem Meter ist. Allerdings kann man nicht einfach sagen, dass die reale Kette also um diesen Betrag kürzer sein kann, da sich insgesamt die Form des Kettenverlaufs ändert, auch in Abhängigkeit davon, wo das Reitgewicht angebracht ist. Es ist am effektivsten dicht am Anker, aber so, dass es noch frei schwimmen kann. In diesem Fall erreicht man eine Reduktion der benötigten Kettenlänge um fast FR/m Meter. Jedoch ist der Gewinn eher klein: Ein Reitgewicht von 10 kg im Wasser führt bei einer 10 mm Kette mit m = 2 kg/m nur zu einer Verkürzung von etwas weniger als 5 m.

Wenn Reitgewicht und Kette aus dem gleichen Material sind, kann man also aus Prinzip keine Gewichtsersparnis für das Boot erzielen, indem man Gewicht von der Kette zum Reitgewicht allokiert. Dies funktioniert nur dann, und auch hier nur in begrenztem Maße, wenn das Reitgewicht aus einem Material mit deutlich höherem spezifischen Gewicht besteht, etwa aus Blei.
Andere, hiervon unberührte, Vorteile eines Reitgewichts sind die Reduktion des Schwoikreisradius, und dass man das Reitgewicht mehr im Zentrum des Bootes lagern kann und nicht am Bug.
Auch der Fall einer Kombination von Kette und Trosse oder auch nur Kette im Wasser und Kette oberhalb der Wasseroberfläche lässt sich mit Hilfe der Kettenkurven berechnen. Hierzu muss man nur zwei solche Kettenkurven mit verschiedenen Parametern a1 und a2 miteinander geeignet verbinden. Da es keine Scherkräfte gibt, muss die Verbindung dieser beiden Kurven „glatt” sein oder, mathematisch ausgedrückt, muss die Kettenkurve an dieser Stelle stetig differenzierbar sein.
Haltekraft der Kette am Boden
Zum Schluss sei noch kurz der manchmal gegebene Rat analysiert, immer 20–30 Meter Kette am Meeresboden liegen zu haben, da dies die Haltekraft erhöhe. Dies ist leider ein Trugschluss. Wenn man eine am Boden liegende Kette über den selbigen ziehen will, muss man eine gewisse Kraft aufwenden, die proportional zum Gewicht der Kette ist, um die Haftreibung zu überwinden – siehe Wikipedia.

Der Proportionalitätsfaktor, häufig µH genannt, hängt vom Material der Kette und der Bodenbeschaffenheit ab. Öl, und in geringerem Maße auch Wasser, verringern die Haftung, und in der Regel findet man Werte µH < 1, was bedeutet, dass eine Kette von 30 Metern Länge und 2 kg Gewicht pro laufendem Meter im Wasser nicht einmal 60 kg zusätzlich zum Anker zur Haltekraft beiträgt — sehr wahrscheinlich sogar deutlich weniger.

Dieser Anker wird in einem guten Untergrund jedoch viele Hundert Kilogramm Haltekraft entwickeln, und somit ist der Effekt der auf dem Meeresboden liegenden Kette bezüglich zusätzlicher Haltekraft marginal. Man kann sich hiervon leicht überzeugen, indem man einige Meter seiner Ankerkette einmal am Strand durch seichtes Wasser zieht und dann auf 30 Meter hochrechnet. Es bedarf keiner großen Kraft.
Oder betrachten wir es einmal so: 60 kg Kettengewicht auf dem Boden, das ist nur das Doppelte oder Dreifache vom Ankergewicht, und bei diesem würde niemand ruhig schlafen, wenn der Anker nur einfach so auf dem Boden rumliegen würde, ohne sich richtig eingegraben zu haben. Warum also sollten uns 60 kg Kette am Meeresboden beruhigen? An ihrer Reibungskraft am Untergrund liegt es nicht, es ist einzig die Tatsache, dass wir noch etwas Spielraum haben und der Wind somit also noch etwas zulegen darf, bevor die Kette nicht mehr waagerecht am Anker angreift.
Fazit
Nun wissen wir also, wie der Mathematiker ankert! Obgleich — ein echter Mathematiker oder Theoretischer Physiker bei diesem Problem zunächst einmal auf sogenannte dimensionslose, skalierte Koordinaten transformieren wird, (x,y) → (x/a,y/a), da man dann nur noch eine einzige Kurve betrachten muss, die universelle Kettenkurve. Für uns ist dies jedoch unpraktisch.
Für den Allgemeingebrauch ist wichtig zu wissen, dass die Faustregel „pro Meter Wassertiefe 3, 4, 5, 6 oder sogar 7 Meter Kette” nur einen Extremfall beschreibt, bei dem die Kette praktisch vollkommen straff gespannt ist und keinerlei Bauch mehr zeigt. Dafür braucht es einen starken Sturm oder eine extrem leichte Kette. Im Grunde besagt diese Faustregel also nur, dass wir hoffen, dass der Anker noch halten wird, wenn die Kette mit einer Steigung 1:3, 1:4, etc. am Anker ansetzt und anfängt, selbigen aus dem Untergrund herauszuhebeln. Ob dies in einem Sturm passiert, hängt logischerweise vom Anker und vom Untergrund ab, und die Mathematik wird uns hier wenig weiterhelfen, zumal wir die genaue Form des Ankers nicht spezifiziert haben.
Andererseits, die Gleichungen 4, 5, 7 und 8 oder auch einfach die Abbildungen 7 bis 11 beschreiben auch den Fall, wenn der Wind nicht ganz so hart bläst. Wenn man also insbesondere nur für ein paar Tage ankert und weiß, wie das Wetter sich entwickeln wird und kein Sturm zu erwarten ist, dann muss man vielleicht nicht die sehr konservative Sturmregel 1 : X nehmen, sondern kann die obigen Formeln verwenden und auch auf ein paar Metern mehr Wassertiefe noch sorgenfrei ankern, wenn sonst kein Platz mehr frei ist.
Die von Sönke und Judith Roever propagierte Faustformel, Kettenlänge L = Y + Konstante, kann hierbei eine brauchbare erste Näherung sein bei größeren Wassertiefen Y und nur moderatem Wind. Allerdings hängt die Konstante sowohl von der Größe des Schiffes als auch von der Windstärke ab, und so ist es nicht viel aufwendiger, die genaue Formel zu verwenden. Mehr als Addieren, Multiplizieren und Wurzel ziehen ist es nicht.

So lautet die Formel und ich brauche den Parameter a ja nur einmal für mein Schiff zu tabellieren, wie beispielsweise in Tabelle 1, die ich hier noch einmal aufführe.

Beispiel: Bis 7 Bft., Aeff = 5 m² und Wassertiefe 10 Meter. Nach der Tabelle ist a = 44,9. Demnach ist L dann 31,6 Meter.

Abschließend sei jedoch noch einmal betont, dass ich hier die minimal benötigte Kettenlänge ausgerechnet habe unter der Randbedingung, dass die Kette noch waagerecht am Anker angreift und selbiger somit maximal halten kann (und dies auch tut), und es zudem keinen Wellengang gibt.
Es schadet jedoch nicht, noch etwas mehr Kette zu stecken, wenn möglich, falls der Wind unerwartet auffrischen sollte, oder um etwas mehr Dämpfung durch die Kette zu ermöglichen und so dem berüchtigten Einrucken derselben entgegenzuwirken. Wenn der Anker trotz allem doch ausbrechen sollte, lag es zumindest nicht an einer zu kurzen Kette. Abhilfe würde in einem solchen Fall nur ein größerer beziehungsweise stärkerer Anker oder ein zweiter Anker bringen.
























Tolle Abhandlung, endlich ist mal jemand dem Thema richtig auf den Grund gegangen! Wenn ich alles richtig verstanden habe, gelten die Formeln allerdings nur unter der Annahme eines ebenen Ankergrundes. Bei abfallenden Ankergründen, wie man sie ja leider auch hin und wieder vorfindet, wären dann wohl noch kompliziertere Formeln notwendig – oder man steckt einfach etwas mehr Kette…
Das stimmt. Könnte man auch noch berücksichtigen mit einer entsprechenden Steigung der Kette am Anker, aber dann hätte man sehr viele Parameter zu jonglieren… 🙂 Also, etwas mehr Kette ist dann in der Tat einfacher. Wobei ich starke Abhänge immer versuche zu vermeiden. Wir hatten da in der Karibik einmal einen krassen Fall…
Also, ich habe da noch einmal etwas drüber nachgedacht. Das Problem des schiefen Untergrunds kann man im Grunde mit den Formeln aus dem Abschnitt „Was passiert, wenn die Kette nicht mehr waagerecht am Anker angreift?“ behandeln. Man passt die dort angenommene Steigung einfach der Steigung des Untergrunds an… Also einfach, dass der Anker die Steigung des Untergrunds hat.
Puuh…..wenn ich mir das so ansehe, bleib´ ich lieber im Hafen
Da habt Ihr Euch ja ordentlich Mühe gemacht und ich würde sagen, dass hat sich mehr als gelohnt. Natürlich treffen hier auch wieder Theorie und Praxis auf einander, aber endlich ist das Glas mal für beide Seiten halb voll oder halb leer, wie es jeder sehen will und endlich habe ich eine Grundlage. Also raus aus der grauen Theorie und rein in gesicherte Grenzwerte plus Idealismus. Vielen Dank.
Merci! 🙂
Mir fällt auf, dass nicht die Höhe des Bugs (Ankerkettenaustritt), der ja ca. 1,5 m über der Wasserlinie berücksichtgt wird. Bei 3 m Wassertiefe hat das schon ehrhebliche Auswirkungen auf die Wahl der Ankerketten-Läng – sei es per Faustformel oder exact hergeleitet.
Das stimmt, aber man kann einfach meine Formel von dem Punkt des Eintritts der Kette in das Wasser verwenden, und dann die Länge bis zum Bug oben hinzuaddieren.
Einfach sehr interessant.Danke.
Merci! 🙂
Ja aber Hallo, das ist dochmal eine sehr vernünftige, wissenschaftliche und dennoch am Ende praxisnahe Abhandlung. Ich als Ingenieur mit Grundstudium Physik könnte das sicherlich nachvollziehen, bin nur leider aus der Übung 🙂
Werde mit die Tabelle für mein Schiff anfertigen und eventuell 10m Reserve für Welle, Kette über der Wasserlinie und Kette am Boden für horizontalen Zug hinzufügen.
Das einzige was ich nicht machen werde ist meine Stahlkette durch eine Eisenkette zu ersetzen. J
Gruß Jürgen
😀
HALLO HERR Wagner,
Vielen Dank für Ihren Artikel. Könnten Sie bitte noch darstellen, wie sie nach Formel 7 den Wert von a in der Tabelle 1 ermittelt haben.
Da Sie leider für 8mm Ketten keine Tabelle beigefügt haben, „musste ich zum Äußersten greifen“ und selbst rechnen. Dabei bin ich dann leider gescheitert ihre Werte der 10mm Ketten nachzurechnen.
Daher meine Bitte den Rechenweg vom Winddruck in N/qm zu Werten von a aufzuzeigen.
Vielen Dank für Ihre Bemühungen im Voraus!
Also, a = F_W / ( m*g) und F_W = A_eff * P_stau. m*g ist für eine 10 mm Kette 2 kg/m und für eine 8 mm Kette laut Internet 1.22 kg/m. P_stau für 2 BFT ist laut Tabelle 6.6 N/m^2. Das muss man durch g, also 9.81, dividieren, um es in Kg / m^2 zu haben. Also ist F_W = A_eff * 6.6 / 9.81 für diesen Fall, und somit erhält man für A_eff = 5 m^2: F_W = 3.36. Bei einer 10 mm Kette mit m * g = 2 kg/m folgt dann a = 3.36/2 = 1.68,… Mehr lesen »
Lieber Herr Wagner, das ist ein hoch interessanter Artikel; besonders für mathemathisch-physikalisch Vorgebildete. Leider bin ich das nicht. Mich plagen beim Ankern ganz andere Probleme: welcher Abstand zum Ufer? wie weit muss ich fahren, um den Anker zu fallen zu lassen und wo werde ich sein wenn die Kette draußen ist? Reicht dann der Abstand zum Nachbarn/Ufer noch, auch wenn der Wind dreht? Die Wassertiefe weiß ich auch erst im allerletzten Moment… Ich bewundere Menschen, die das alles und Ihre Berechnungen in dieser Situation auf die Reihe kriegen. Ich bin wohl einfacher gestrickt und brauche eine ganz simple Faustformel –… Mehr lesen »
Ja, das verstehe ich alles, und die Probleme habe ich auch. Die Wassertiefe weiss man allerdings von Anfang an. Es ist die Tiefe dort, wo der Anker fällt, und nicht dort, wo das Schiff zu liegen kommt.
Hallo Uli,
ich will am Vordeck auch keine Wurzeln ziehen. Als Kompromiss von genau und einfach verwende ich die Formel: Kettenlänge = 20m+doppelte Wassertiefe. Je nach Situation kann man dann noch etwas nachjustieren…
Also, dem kann nun etwas geholfen werden… Ich habe diese Rechnungen nun auch als App verfügbar gemacht. iPhone und iPad sind schon da, Android wird folgen… 🙂
https://trimaran-san.de/anchor-chain-calculator/
Und nun gibt es auch eine deutsch-sprachige Web Seite dazu: https://trimaran-san.de/ankerketten-rechner/
Super Artikel. Vielen Dank Martin
Da habe ich noch etwas dran zu kauen, um alles zu verstehen und nachzuvollziehen.
Die Betrachtung der waagerecht angreifenden Kette ist schlüssig. Interessant der geringe Effekt der Wassertiefe.
Aus praktischer Sicht und Erfahrung kann ich die Schlüsse sehr gut nachvollziehen.
Merci!
Sehr interessanter Beitrag, nach mehr als 1000 Ankermanövern und noch etlichen hundert beobachteten kann ich dazu nur sagen, was nützt die richtige Kettenlänge, wenn der Anker ungeeignet oder zu klein dimensioniert ist. Wir fahren auf unserem 4Ton Katamaran einen 20 kg Bügelanker, der richtig eingefahren auch schon Böen jenseits der 30kn mühelos weggesteckt hat auch bei nur 2-facher Kettenlänge im Verhältnis zu Wassertiefe. mehr Kette war aufgrund anderer Ankerlieger, Nähe zum Ufer nicht möglich. Leider nehmen viele Schiffsbesitzer das nicht richtige Eingraben ihrer vor allem CQR Anker als Gott gegeben und denken nicht über einen Wechsel des Ankertyps nach, stecken… Mehr lesen »
Absolut korrekt. Wir haben einen 35 kg Spade Anker bei der SAN, der gräbt sich eigentlich immer gut ein. Die Werft hatte einen kleineren Anker empfohlen, aber das ist Unsinn. 35 kg ist Minimum.
Lieber Mathias,
ich freue mich dass das Thema Ankerketten wieder einmal aufgenommen wird. Ich habe mich lange mit diesem Thema beschäftigt und in der Zeitschrift „Palstek“ ab der Ausgabe 5/2007 Artikel dazu geschrieben. Die meisten deiner Berechnungen findet man dort auch.
Ein Thema kommt zu kurz bei deiner Abhandlung: Die meisten Fälle von ausreißenden Ankern passieren bei Wellen. Daher habe ich schon in meinem ersten Artikel auch das Thema „dynamisches Ankern“ angesprochen.
Mit besten Grüßen
Harald Melwisch
harald.melwisch@kabsi.at
Hallo Harald, ja, es musste schon Artikel zu diesem Thema geben, ich konnte es mir nicht vorstellen, dass das nicht schon alles behandelt worden ist, aber ich konnte seinerzeit nichts finden. Ich versuche mal, Deinen Artikel in Palstek zu finden. Und ja, Wellen sind ein Thema, welches ich nicht behandelt hatte. Es gibt auch einen Franzosen, dessen Web Page dazu was sagt. Seine Seite hatte ich erst nach Schreiben meines Artikels gefunden: http://alain.fraysse.free.fr/sail/rode/rode_b.htm. Dort findet man irgendwo auch meine Formeln wieder. Aber ich finde meinen Text klarer… 😉
Lieber Harald, vielen Dank für den Austausch per Mail. Ich habe nun auf unserer web page unter fun facts ein update eingestellt, welches auch das dynamische Ankern mit berücksichtigt und komme auf die gleichen Ergebnisse wie Du. Ich bin wieder etwas formellastiger, aber die Formeln bleiben recht einfach.. 😉 Die Ergebnisse zu dem Ankern im flachen Wasser sind schon erstaunlich und waren mir vorher nicht so bewusst. Sie sind aber für ein sicheres Ankern definitiv wichtig zu wissen. Vielleicht kann ich ja Sönke überreden, noch einmal einen Update bei Blauwasser zu machen. VLG Mathias
So, nun ist es vollbracht. Ich habe nun auch Wellenschlag in den Formeln berücksichtigt, welches zum dynamischen Ankern führt. Vielen Dank and Harald, mich darauf aufmerksam zu machen. Das Ganze wird spannend in flachem Wasser… Wer mehr wissen möchte, auf meiner home page unter Fun Facts sind kurze Digests für verschiedene Bootsgrößen vorhanden (Englisch). Das ausführliche Paper ist auf Deutsch dort vorhanden, aber die kurzen englischen sind sicherlich besser geeignet…
Hallo, gibt es eine Excel Vorlage oder eine App mit der man für sein Schiff all das berechnen kann und diese Diagramme erstellen kann?
Also, ich habe bisher keine solche Excel Vorlage erstellt. Aber auf unserer Web Page unter https://trimaran-san.de/die-kettenkurve-oder-wie-ein-mathematiker-ankert/ gibt es inzwischen einen ganzen Haufen von kurzen Digests für verschieden große Boote und verschieden dicke Ketten. Da sollte schon was passendes dabei sein. Auf der gleichen Seite unten sind auch links zu Catenary calculators, die ich inzwischen entdeckt habe. Ein link dort hat auch Excel Tabellen, aber die habe ich nicht ausprobiert. Über eine App habe ich nachgedacht, vielleicht bastelt mein Sohn mal eine. 🙂
Jaaa, 🙂 🙂 🙂 eine App gibt es nun seit einigen Tagen: AnchorChainCalculator : https://trimaran-san.de/anchor-chain-calculator/ . Zunächst nur für iPhone und iPad, aber wenn ihr im Kommentar mir sagt, ihr wollt alle Android, dann setze ich mich da vielleicht auch noch mal dran… 😉
Und nun gibt es auch eine deutsch-sprachige Web Seite dazu: https://trimaran-san.de/ankerketten-rechner/
Super erklärt, auch wenn mein Matheunterricht bereits 45 Jahre zurück liegt. Aber eine Frage habe ich doch noch. Wie verhält sich ein 14 Tonnen schweres Schiff gegenüber einem KS-Schiff mit nur z.B. 5 Tonnen Verdrängung? Alle andere Parameter sollen gleich bleiben. Oder trifft hier Archimedes Prinzip so zu, dass diese Differenz total zu vernachlässigen ist?
Vielen Dank! Im Rahmen des hier verwendeten Models sind beide Boote gleich, solange sie die gleiche Windangriffsfläche haben und die gleiche Kette verwenden. Aber wenn man dann weiter geht und z.B. Schwell berücksichtigt, dann braucht man auch das Gewicht des Schiffes, um aus der Geschwindigkeit des Schiffes am Anker die kinetische Energie zu berechnen. Siehe https://trimaran-san.de/die-kettenkurve-oder-wie-ein-mathematiker-ankert/, was allerdings vielleicht schon zu viel Stoff ist – mir sind da etwas die Pferde durchgegangen… 😉 Zudem kann ich nun eine App anbieten, die das alles berechnen kann: https://trimaran-san.de/anchor-chain-calculator/ 🙂
Und nun gibt es auch eine deutsch-sprachige Web Seite dazu: https://trimaran-san.de/ankerketten-rechner/
Super Abhandlung, vielen Dank
Frage an den Autor: wenn ich Gleichung 9 nach a auflöse (a=x1/arsinh(y1)), müsste ich doch über eine Messung des Kettenwinkels (y1) direkt am Boot den Wert von a bestimmen können und mit dem gemessenen Wind den Windwiderstand berechnen evtl. gemittelt über verschiedene Windstärken).
Oder sind meine Annahmen hierbei falsch.
Thomas Rumpf
Danke! (Sorry, dass ich so spät antworte – ich erhalte keine Nachricht, wenn ein neuer Kommentar reinkommt.) Und ja, das ist korrekt, das ist eine Möglichkeit, den Parameter a zu bestimmen. Aber die Messung ist nicht ganz trivial und mit großem Fehler verbunden. Also sollte sie mehrmals wiederholt werden und unter verschiedenen Bedingungen.
LG, Mathias
Hallo! Vielen Dank für diesen Beitrag, den ich, obwohl ich zwischendurch mehrmals ausgestiegen bin, als wirklich exzellent erachte. Ich beiß mich gerade noch durch mehrere Deiner Gleichungen, Abi ist laaaange her, und hoppla, es macht Spaß! Danke für die Mühe!
Hallo Peter, danke für dieses nette Feedback! Ich finde die Mathematik um die Kettenkurve einfach wunderschön. Es passt alles so schön zusammen. Und letztendlich wird die Physik wieder ganz einfach, wenn man sich einmal durchgebissen und es verstanden hat. Dann lassen sich die grundlegenden Prinzipien, wann eine Kette gut funktioniert und wann nicht, ganz einfach erklären. Dieses Wissen hilft mir nun schon ein ganzes Jahr, sicherer zu Ankern – und wir sind 340 Tage im Jahr vor Anker… 🙂 Mein Mathematiklehrer in der Schule schrieb einmal eine Gleichung an die Tafel, -1 = Exp(i * pi), und sagte, die Gleichung… Mehr lesen »
Grundsätzlich eine Super Abhandlung. Ich habe einmal begonnen, alle Faktoren die für sicheres Ankern notwendig sind zu listen. Nach 100 Faktoren habe ich abgebrochen! Zumal die ganzen Daten für den Mathematiker nicht verfügbar sind und schon gar nicht für den Skipper irgendwo am Globus! Frage z.B. den Hersteller deines Schiffes nach dem Luftwiderstandsbeiwert deines Schiffes! Wie stellst du bei einem Charterschiff die AKTUELLE Bruchfestigkeit der Ankerkette fest (kann ja im Betrieb schon einmal stark belastet worden sein, wodurch die Bruchfestigkeit stark reduziert wurde!)? Wie ermittelst du die zu erwartende Windstärke? Wie zuverlässig ist die Wettervorhersage? Viel Spaß. Man landet zwangsweise… Mehr lesen »
Hallo Franz. Die 8 Grad beziehen sich auf die tolerierte Verringerung der maximalen Haltekraft eines Ankers. Das ist sicherlich von Hersteller zu Hersteller verschieden, das kann ich nicht beurteilen. Wichtig ist es aber auch, Lastspitzen zu vermeiden, bei denen die Kette steif kommt, im starken Schwell oder Bö. Dann wird über diese mit 8 Grad ansteigende Kette auf einmal ein Vielfaches der normalen Last übertragen und der Anker bricht trotz der „nur“ 8 Grad aus. Auf Blauwasser.de wird es hierzu demnächst einen weiteren Artikel geben.
So, nun ist die Erweiterung auf das dynamische Ankern und die Beschreibung meiner AnchorChainCalculator App auf Blauwasser verfügbar: https://www.blauwasser.de/ankergeschirr-berechnen-ausbrechen-app 🙂
Sehr interessante und aufschlussreiche Analyse, die aber einen statischen Zustand annimmt.
Die reale Situation weicht davon aus zwei Ursachen ab.
1. Wellen am Ankerplatz. Dieser Einfluss ist vermutlich gering, wenn man mit Land in Luv ankert.
2. Einrucken am Umkehrpunkt der Schwojenbewegung. Hier scheinen mir erhebliche zusätzliche Kräfte aufzutreten, die sich aus der Querstellung der Yacht zum Wind ergeben und eine erhöhte Aeff zur Folge haben sollten.
Frage an Mathias: Hast Du für diese Fälle Erfahrungswerte für einen Sicherheitsfaktor y wie z.B. y (45°)= Aeff45°/Aeff0° wobei die °-Zahl den Windeinfallswinkel am Wendepunkt der Schwojbewegung kennzeichnet?
Hallo Klaus. Punkt 1: Inzwischen bin ich hier weiter: Der dynamische Aspekt wird über einen neuen Parameter „Velocity at Anchor“ abgedeckt. Dieser bezieht sich nicht direkt auf die Wellen, sondern auf den Effekt, den starke Wellen oder auch eine Böe haben: Das Boot beschleunigt und bekommt kinetische Energie, welche irgendwie absorbiert werden muss. Dies kann einen starken Effekt haben. Stichwort Fallböen. Zum 2. Punkt: Erfahrungswerte hierzu sind mir nicht bekannt, aber man kann natürlich einen Sicherheitsfaktor einfach annehmen, welcher die erhöhte Windangriffsfläche von der Seite berücksichtigt. Da so eine Querstellung nicht stabil ist, sondern Drehmomente das Boot wieder zum Wind… Mehr lesen »